Rezultat rekonstrukcji modelu przestrzennego, wykonanej za pomocą funkcji dostępnych w zakresie Reverse Engineering jest zwykle nieparametryczny. To oczywiście oznacza, że nie jest możliwa łatwa i szybka modyfikacja kształtu takiego modelu. Ale czy zawsze tak musi być?

Andrzej Wełyczko

Jeśli rekonstruowany element ma kształt zdefiniowany przez zaawansowane powierzchnie z krzywizną zmieniającą się w obu kierunkach głównych (double curvature surfaces), to nie ma jednoznacznej metody „odtworzenia” ich parametrycznej definicji. Problem jest jednak znacznie łatwiejszy dla części pryzmatycznych, czyli takich, których kształt jest opisany za pomocą powierzchni kanonicznych (płaskich, cylindrycznych, stożkowych lub wyciąganych). Powierzchnie kanoniczne to takie, dla których w każdym ich punkcie promień krzywizny przynajmniej w jednym kierunku ma wartość nieskończoną.

Rys. 1

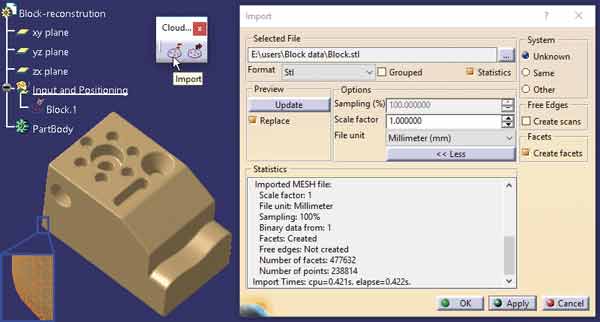
Rozważmy przykład kostki, której rezultat skanowania 3D w formacie STL jest importowany do CATIA V5 (Rys.1). Można oczywiście kwestionować konieczność rekonstrukcji tak prostego detalu, który łatwo zmierzyć, a wyniki pomiarów uwzględnić w procesie konstruowania „od zera”. Mam jednak nadzieję, że metoda opisana poniżej chociaż w części zainspiruje tych, którzy problemy rekonstrukcji modelu rozwiązują na co dzień.
Skan 3D (niezależnie od formatu) umożliwia zdefiniowanie modelu przestrzennego za pomocą siatki trójkątów. Pewnie dlatego skrót STL (STereo Lithography), jako najstarszy z formatów stosowanych w technikach Rapid Prototyping oraz Reverse Engineering, ma także inne rozwinięcia: Standard Triangle Language lub Standard Tessellation Language. Taka siatka może być wygładzana, filtrowana, ręcznie lub automatycznie naprawiana, optymalizowana, …itd. W tym przypadku ten etap pominę, bo te operacje nie mają wpływu na metodę opisaną poniżej.
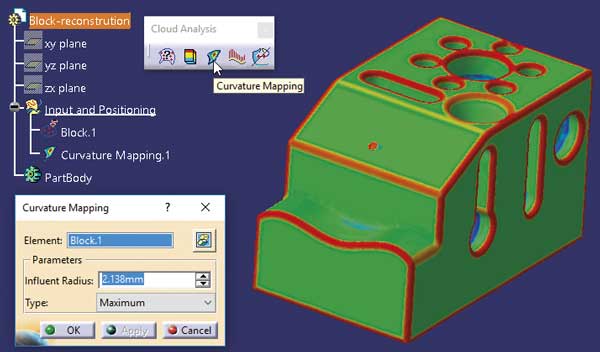
Przed rozpoczęciem procesu rekonstrukcji warto wykonać analizę rozkładu krzywizny dla zaimportowanej siatki (polecenie Curvature Mapping dostępne w środowisku na rysunku 2).

Rys. 2

Jeśli taka analiza zostanie wykonana dla Type = Maximum, to jej rezultatem jest identyfikacja obszarów o różnych promieniach krzywizny:

• obszary czerwone lub niebieskie: „klasyczne” zaokrąglenia krawędzi,
• obszary zielone: powierzchnie płaskie, cylindryczne, stożkowe lub wyciągane, czyli takie, których krzywizna przynajmniej w jednym kierunku jest zerowa.

Dzięki takiej analizie można zaplanować kolejne etapy procesu rekonstrukcji, bo wiemy gdzie zdefiniować powierzchnie kanoniczne, a gdzie powierzchnie z krzywizną w obu kierunkach głównych.
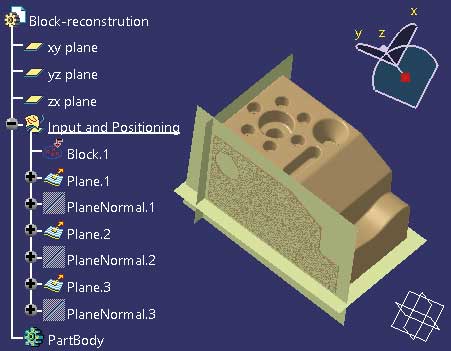
Jeśli celem jest uzyskanie przynajmniej częściowo parametrycznego modelu powierzchniowo-bryłowego, to warto zdefiniować taką transformację siatki STL, która ustali jej położenie na płaszczyznach głównych przestrzeni roboczej. W tym celu trzeba wykonać rekonstrukcję kilku elementów geometrycznych, które posłużą do zdefiniowania takiej transformacji. Mogą to być na przykład trzy płaszczyzny (Rys. 3), które w kolejnym kroku będą powiązane z płaszczyznami głównymi modelu (xy plane, zx plane oraz yz plane).

Rys. 3

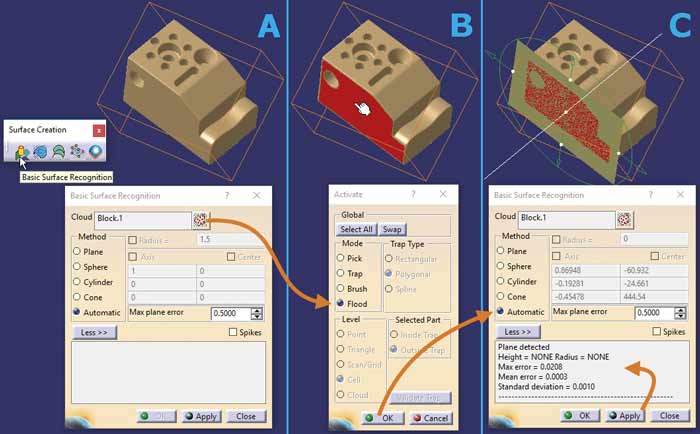
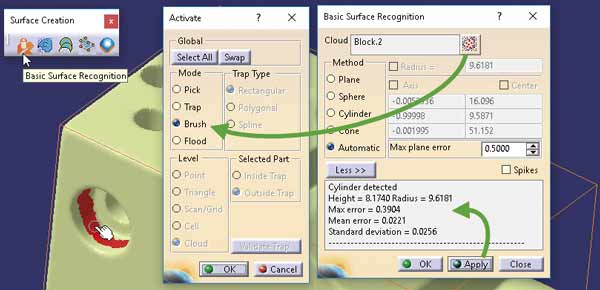
Każda powierzchnia kanoniczna może być „odtworzona” za pomocą polecenia Basic Surface Re­cognition. W tym celu, po wskazaniu siatki (Rys. 4 A) należy aktywować jej fragment (dla powierzchni płaskich najlepiej zastosować Mode = Flood – Rys. 4 B), a następnie obrócić/rozciągnąć proponowaną przez system powierzchnię do takiego położenia/wielkości, która jest wymagana (Rys. 4 C). Skanowanie 3D nigdy nie jest perfekcyjne i dlatego zawsze wystąpi błąd rekonstrukcji – tu Max error = 0.0208. Ważne jest to, aby ten błąd nie był zbyt duży, na przykład mniejszy niż 0,1mm.

Rys. 4

Transformacja siatki może być zdefiniowana za pomocą polecenia Align with Constraints, dla którego zdefiniowano relacje: Plane.3 – xy plane, Plane.1 – zx plane oraz Plane.2 – yz plane (Rys. 5).

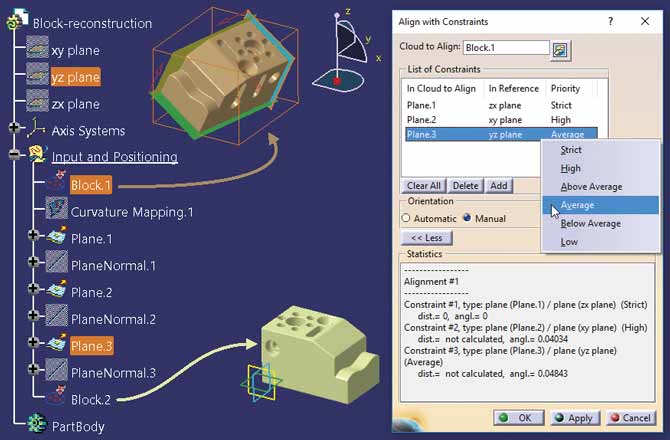
Rys. 5

W polu Statistics okna Align with Constraints system prezentuje raport, z którego jasno wynika, że zadane pary płaszczyzn nie są do siebie idealnie równoległe. Na przykład dla pary Plane.1 – zx plane mamy: dist.=not calculated, angl. – 0.01697. Gdyby taka dokładność była zbyt mała, to po wyznaczeniu płaszczyzny Plane.1 należałoby (za pomocą polecenia Plane w środowisku GSD) zdefiniować dwie płaszczyzny prostopadłe do Plane.1, umieszczone jak najbliżej odpowiednich ścian siatki Block.1.
Po wykonaniu polecenia Align with Constraints siatka STL jest „dopasowana” do płaszczyzn głównych modelu i dlatego w łatwy sposób można zdefiniować kontur prostokątny (Sketch.1 na rysunku 6) oraz bryłę Pad.1, która w całości zawiera siatkę Block.2.

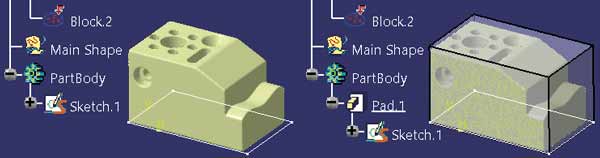
Rys. 6

Kształt bryły może i powinien być zmodyfikowany za pomocą kolejnych powierzchni (tu: Plane.4 na rysunku 7), którą, podobnie jak poprzednio, zdefiniowano stosując polecenie Basic Surface Recognition.

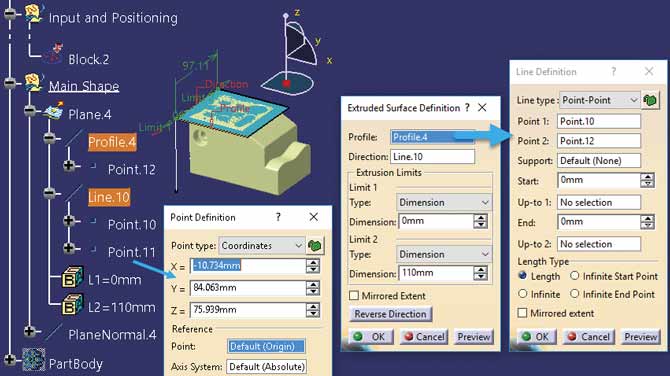
Rys. 7

Czy taka definicja powierzchni płaskiej jest parametryczna? Powierzchnia Plane.4 powstała w wyniku wyciągania linii Profile.4 w kierunku linii Line.10. Obie linie są zdefiniowane pomiędzy punktami, których definicja jest parametryczna, a więc i one, i powierzchnia są parametryczne. Definicja kolejnych powierzchni płaskich, odcięcie „zbędnych” fragmentów oraz modyfikacja bryły za pomocą polecenia Split (Rys. 8) nie wymaga chyba komentarza.

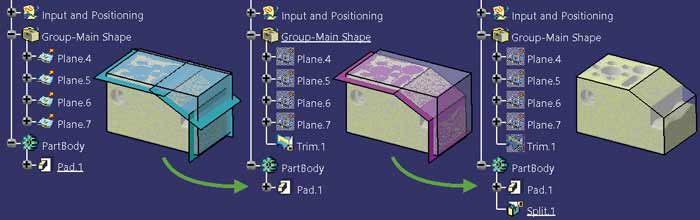
Rys. 8

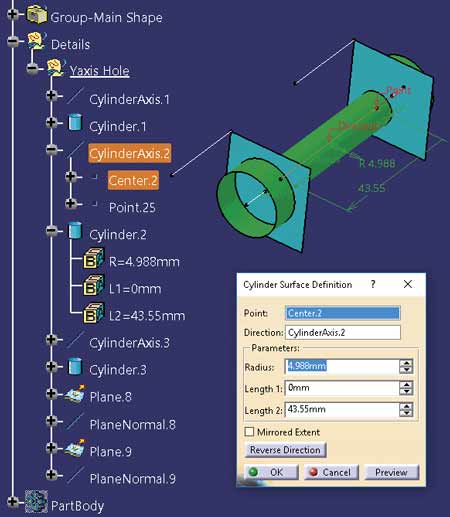
Odtworzenie szczegółów konstrukcyjnych (otwory i wybrania) można także wykonać za pomocą polecenia Basic Surface Recognition (pod warunkiem, że ich kształt jest kombinacją powierzchni kanonicznych). Na przykład otwór stopniowy (Rys. 9 i 10) można zrekonstruować za pomocą trzech powierzchni cylindrycznych i dwóch powierzchni płaskich. Definicja fragmentu siatki, który posłuży do rekonstrukcji powierzchni cylindrycznej lub stożkowej może być wykonana za pomocą polecenia Activate w trybie Mode = Brush albo w trybie Mode = Trap (Rectangular lub Polygonal).

Rys. 9

Rys. 10

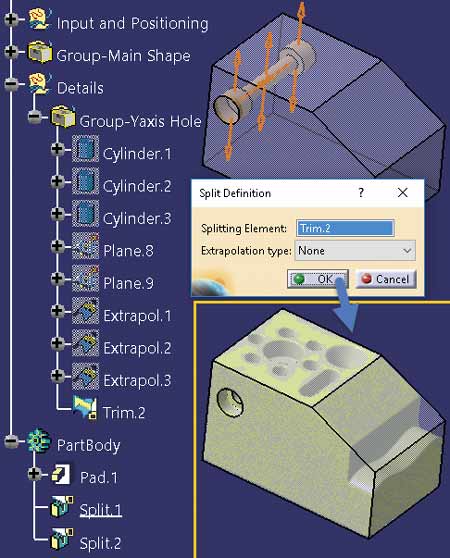
Także w tym przypadku zrekonstruowane powierzchnie cylindryczne są parametryczne, czyli można modyfikować ich parametry (promień, punkt początkowy i końcowy osi). Podobna procedura, czyli rekonstrukcja powierzchni kanonicznych, ekstrapolacja tych powierzchni, wykonanie polecenia Trim (odcięcie „zbędnych” fragmentów oraz połączenie w jedną powierzchnię) i wykonanie polecenia Split w celu modyfikacji kształtu modelu bryłowego może być zastosowana dla pozostałych szczegółów konstrukcyjnych.

Rys. 11

Rezultat takiej procedury rekonstrukcji jest parametryczny, ale nie jest to jedyne z możliwych rozwiązań. Jaki obiekt jest najczęściej stosowany w modelach parametrycznych? Odpowiedź jest chyba oczywista: kontur, szkic (Sketch w nomenklaturze systemu CATIA V5).
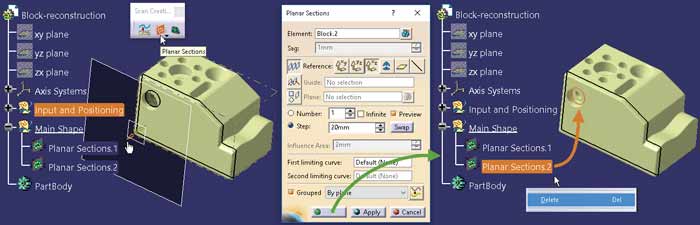
W procesie rekonstrukcji płaskie „krzywe” mogą być zamienione na kontury, czyli obiekty typu Sketch. Użyłem określenia „krzywe”, bo rezultat wykonania polecenia Planar Sections (z wyłączonym trybem Flip to curve creation) jest tylko zbiorem punktów siatki zredukowanym do wybranej płaszczyzny, a nie rzeczywistą krzywą (Rys. 12).

Rys. 12

Jeśli, co oczywiste w pierwszym kroku, celem jest definicja konturu, który określa zewnętrzny kształt rekonstruowanego elementu (bez szczegółów konstrukcyjnych), to istotnym w określeniu tego kształtu elementem jest obiekt Planar Sections.1 (Planar Sections.2, jako nieistotny na tym etapie procesu rekonstrukcji, może być usunięty).
W kolejnym kroku należy zastosować polecenie Sketch from Scan z aktywnym trybem Primitive, (Rys. 13).

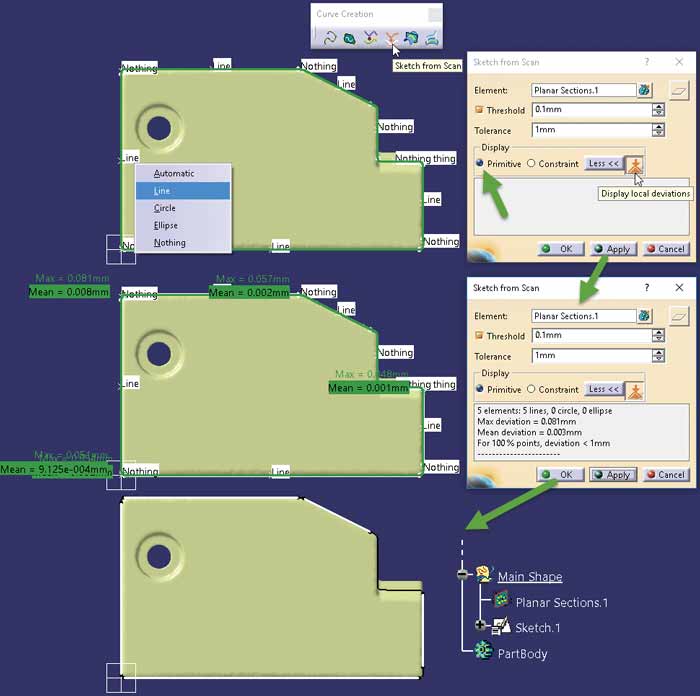
Rys. 13

W tym trybie rekonstruowany kontur może być zbudowany z odcinków linii prostej, łuku okręgu lub elipsy. Dla każdego segmentu rozpoznawanego konturu wykonanie tego polecenia jest możliwe w trybie automatycznym (Automatic) lub wymuszonym przez konstruktora (Line, Circle, Ellipse lub Nothing – jeśli zaznaczony element nie ma być rozpoznany). Kształt zewnętrzny rekonstruowanej części z powodów metodologicznych nie powinien być definiowany za pomocą skomplikowanych konturów i dlatego zaokrąglenia narożników zostały pominięte, bo te szczegóły geometryczne zostaną zdefiniowane w końcowej fazie rekonstrukcji za pomocą polecenia Edge Fillet w środowisku Part Design.