Gdyby zadaniem konstruktora była precyzyjna konstrukcja geometrii zarysu zęba koła zębatego, to jedynym problemem może być definicja takiej krzywej w systemie CAD.
Andrzej Wełyczko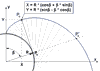 Przypomnę jedynie, że współrzędne dowolnego punktu ewolwenty są opisane układem równań pokazanym na Rys.1. Promień koła zasadniczego R jest tu wielkością stałą, a kąt odwinięcia β jest zmienną, która umożliwia obliczenie współrzędnych dowolnego punktu krzywej (Pe). Czy można zastosować metodę Parallel Curve + Law w definicji ewolwenty koła? Odpowiedź powinna być oczywista. Nie jest to możliwe, bo dowolny punkt ewolwenty (Pe) jest określony dla każdego punktu koła zasadniczego (Pk), ale nie w kierunku prostopadłym do tego koła tylko w kierunku stycznym. Konstrukcja krzywej równoległej do koła zasadniczego byłaby możliwa dopiero wtedy, gdyby dla każdego punktu Pk istniała procedura wyznaczająca punkt P’e ewolwenty w kierunku prostopadłym do koła zasadniczego. To oczywiście jest możliwe po odpowiednich przekształceniach układu równań ewolwenty.
Przypomnę jedynie, że współrzędne dowolnego punktu ewolwenty są opisane układem równań pokazanym na Rys.1. Promień koła zasadniczego R jest tu wielkością stałą, a kąt odwinięcia β jest zmienną, która umożliwia obliczenie współrzędnych dowolnego punktu krzywej (Pe). Czy można zastosować metodę Parallel Curve + Law w definicji ewolwenty koła? Odpowiedź powinna być oczywista. Nie jest to możliwe, bo dowolny punkt ewolwenty (Pe) jest określony dla każdego punktu koła zasadniczego (Pk), ale nie w kierunku prostopadłym do tego koła tylko w kierunku stycznym. Konstrukcja krzywej równoległej do koła zasadniczego byłaby możliwa dopiero wtedy, gdyby dla każdego punktu Pk istniała procedura wyznaczająca punkt P’e ewolwenty w kierunku prostopadłym do koła zasadniczego. To oczywiście jest możliwe po odpowiednich przekształceniach układu równań ewolwenty.
Zanim jednak odrzucimy metodę Parallel Curve + Law trzeba zauważyć, że ma ona dwie bezdyskusyjne zalety: nie jest skomplikowana i generuje krzywą (a nie tylko zbiór punktów) stosownie do wskazanych elementów podstawowych (Curve i Law w oknie Parallel Curve Definition).  Dlatego próbując mimo wszystko zastosować tą metodę także i w tym przypadku można dojść do następujących wniosków:
Dlatego próbując mimo wszystko zastosować tą metodę także i w tym przypadku można dojść do następujących wniosków:
1. Dwa równania oznaczają konieczność zdefiniowania dwóch praw zmienności (Law-X i Law-Y na Rys.2). W obu tych prawach zdefiniowano dwa parametry formalne. Jeden typu Length (odpowiednio X lub Y) i drugi typu Angle (tu BETA). Aby uniknąć konfliktu jednostek równania ewolwenty powinny być zmodyfikowane do następującej postaci:
X = R ∙ (cos(BETA) + PI ∙ BETA / 180deg ∙ sin(BETA))
Y = R ∙ (sin(BETA) - PI ∙ BETA / 180deg ∙ cos(BETA))
2. Dwa prawa zmienności współrzędnych X i Y dowolnego punktu ewolwenty można zastosować w definicji dwóch krzywych pomocniczych. Ale jaka krzywa powinna być wskazana jako podstawowa w definicji krzywej równoległej?
3. W jaki sposób zastosować krzywe pomocnicze krzywe Parallel.1 i Parallel.2 w definicji krzywej na płaszczyźnie wyznaczonej przez krzywą Koło zasadnicze? Tu oczywiste powinno być zastosowanie sekwencji poleceń Combine + Projection:
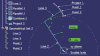 Metoda Parallel Curve + Law została tu zmodyfikowana do postaci 2 x (Parallel Curve + Law) + Combine + Projection, a rezultat jej zastosowania do krzywej Line.1 (czyli krzywa Project.1) jest ewolwentą krzywej Koło zasadnicze. Niestety taka metoda generuje krzywą o ograniczonej długości, bo krzywa Project.1 ma dla zadanej wartości R zawsze taką samą długość – L=R/2. Inaczej mówiąc wartość kąta odwinięcia ewolwenty β może się zmieniać tylko w zakresie od 0° do 180°/PI=57,296° (Rys.6).
Metoda Parallel Curve + Law została tu zmodyfikowana do postaci 2 x (Parallel Curve + Law) + Combine + Projection, a rezultat jej zastosowania do krzywej Line.1 (czyli krzywa Project.1) jest ewolwentą krzywej Koło zasadnicze. Niestety taka metoda generuje krzywą o ograniczonej długości, bo krzywa Project.1 ma dla zadanej wartości R zawsze taką samą długość – L=R/2. Inaczej mówiąc wartość kąta odwinięcia ewolwenty β może się zmieniać tylko w zakresie od 0° do 180°/PI=57,296° (Rys.6). W przypadku ewolwenty taka ograniczona długość krzywej nie stanowi problemu, bo do konstrukcji zarysu zęba potrzebny jest tylko jej początkowy fragment (Rys.7). W przypadku ogólnym czyli wtedy, gdy krzywa jest opisana układem dwóch równań i wymagana jest dowolna długość krzywej metoda 2 x (Parallel Curve + Law) + Combine + Projection nie może być zastosowana.
W przypadku ewolwenty taka ograniczona długość krzywej nie stanowi problemu, bo do konstrukcji zarysu zęba potrzebny jest tylko jej początkowy fragment (Rys.7). W przypadku ogólnym czyli wtedy, gdy krzywa jest opisana układem dwóch równań i wymagana jest dowolna długość krzywej metoda 2 x (Parallel Curve + Law) + Combine + Projection nie może być zastosowana.
W takich przypadkach pozostaje zastosowanie metody przybliżonej. Określenie „metoda przybliżona” jest trochę mylące, bo sugeruje, że rezultat jest niskiej jakości. Tymczasem dokładność przybliżenia ewolwenty za pomocą krzywej typu Spline zależy od liczby (gęstości) punktów wskazanych w jej definicji. Oczywiście współrzędne kolejnych punktów krzywej mogą i powinny być obliczone na podstawie zdefiniowanych wcześniej praw zmienności: Law-X i Law-Y. Na przykład dla punktu początkowego ewolwenty  (Point.2 na Rys.8 został zdefiniowany w trybie Point type = On Plane i dlatego ma tylko dwie współrzędne H i V) mamy zdefiniowane następujące formuły obliczeniowe:
(Point.2 na Rys.8 został zdefiniowany w trybie Point type = On Plane i dlatego ma tylko dwie współrzędne H i V) mamy zdefiniowane następujące formuły obliczeniowe:
PunktyEwolwenty\Point.2\H = ‘Relations\Law-X’ -> Evaluate(0)
PunktyEwolwenty\Point.2\V = ‘Relations\Law-Y’ -> Evaluate(0)
Jeśli wartość argumentów procedury Evaluate jest zadana jako Real (tu 0 a nie 0deg), to system domyślnie przyjmie, że jest to wartość kąta mierzona w radianach.
Kolejne punkty mogą być zdefiniowane tą samą metodą lub po prostu skopiowane – kopie muszą mieć oczywiście inne wartości argumentów procedury Evaluate.  Na szczęście kopiowanie punktów generuje także kopie formuł, które zastosowano do obliczania współrzędnych punktów. Po zdefiniowaniu odpowiedniej liczby punktów ewolwenty (każdy dla innego argumentu procedury Evaluate) pozostaje jedynie definicja krzywej typu Spline, która jest przybliżonym modelem ewolwenty (Rys.9).
Na szczęście kopiowanie punktów generuje także kopie formuł, które zastosowano do obliczania współrzędnych punktów. Po zdefiniowaniu odpowiedniej liczby punktów ewolwenty (każdy dla innego argumentu procedury Evaluate) pozostaje jedynie definicja krzywej typu Spline, która jest przybliżonym modelem ewolwenty (Rys.9). Tak zbudowany model jest parametryczny (Rys.10), ale możliwa jest tylko zmiana promienia koła zasadniczego R. Nie ma możliwości automatycznego generowania zadanej liczby punktów, bo te zostały zdefiniowane „ręcznie”. Nie można również automatycznie zmniejszyć odległości pomiędzy kolejnymi punktami, bo ich położenie wynika z zadanych „ręcznie” wartości argumentów procedury Evaluate.
Tak zbudowany model jest parametryczny (Rys.10), ale możliwa jest tylko zmiana promienia koła zasadniczego R. Nie ma możliwości automatycznego generowania zadanej liczby punktów, bo te zostały zdefiniowane „ręcznie”. Nie można również automatycznie zmniejszyć odległości pomiędzy kolejnymi punktami, bo ich położenie wynika z zadanych „ręcznie” wartości argumentów procedury Evaluate.
Pat? Nie, definicja ewolwenty może być bardziej inteligentna, ale o tym w kolejnym odcinku.
Andrzej Wełyczko
artykuł pochodzi z wydania 6 (21) czerwiec 2009











