Kontynuując temat rozpoczęty w poprzednim miesiącu chciałbym tym razem skupić się nad metodami konstrukcji krzywych opisanych współrzędnymi biegunowymi.
Andrzej Wełyczko
Gdyby zadaniem konstruktora była konstrukcja krzywki płaskiej, której kształt jest opisany za pomocą spirali Archimedesa, to jedynym problemem może być geometryczna definicja tej krzywej w systemie CAD. Tu przypomnę jedynie, że ogólne równanie takiej krzywej to:
Rx = A ∙ φ; gdzie A jest stałą spirali lub inaczej jej skokiem.
Zalety takiej krzywej w zastosowaniach mechanicznych są oczywiste, bo Rx zmienia się liniowo wraz ze zmianą kąta φ. Inaczej mówiąc jeśli krzywka o takim kształcie obraca się ze stałą prędkością (argument φ rośnie liniowo), to popychacz styczny do krzywki porusza się ruchem jednostajnym (Rx zmienia się wprost proporcjonalnie do φ). W zastosowaniach praktycznych interesująca jest nie cała spirala Archimedesa, czyli cały zakres wartości φ z przedziału (0,∞), ale tylko jej niewielki fragment zaznaczony linią ciągłą na Rys.1:
W punkcie początkowym tej krzywej) Rx(β=0) = R,
Zmiana kąta β (od 0 do π) powoduje liniową zmianę wartości
Rx do Rmax(β=π) = R ∙ (1 + A ∙ β).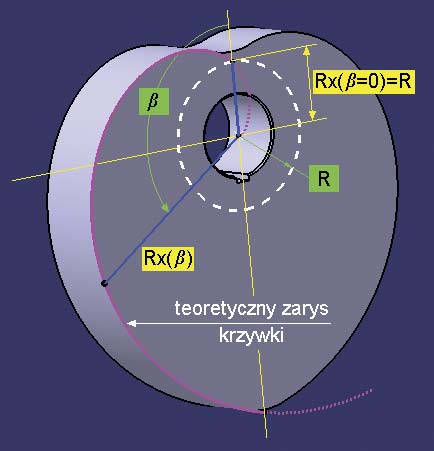
Rys. 1
Załóżmy, że dla krzywej BaseCircle (Rys.2) konstruktor zamierza wykreślić spiralę Archimedesa dla wartości A=1. Jeśli ta krzywa rzeczywiście jest okręgiem, to bez problemu można wyznaczyć płaszczyznę tej krzywej (CamCurvePlane), środek okręgu (BaseCircleCenter) oraz obliczyć jego promień (R=minimumCurvatureRadius(Input\BaseCircle).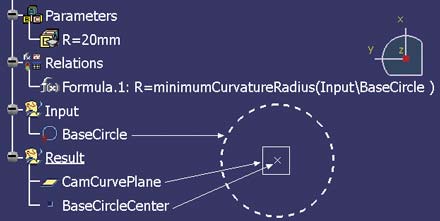
Rys. 2
Jeśli konstrukcja modelu geometrycznego spirali Archimedesa ma być wykonana zgodnie z opisaną w poprzednim odcinku procedurą (Parallel Curve + Law), to nie jest możliwe wskazanie krzywej zamkniętej BaseCircle (Rys.3). 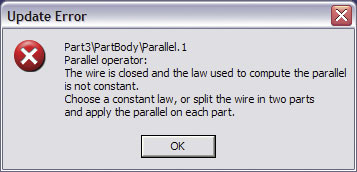
Rys. 3
Dlaczego? Każda krzywa zamknięta ma swój punkt zamknięcia (Closing Point), który jest jednocześnie początkiem i końcem tej krzywej. Jaka wartość parametru Offset polecenia Parallel Curve ma być zastosowana do tego punktu: minimalna czy maksymalna?
- start
- Poprzedni artykuł
- 1
- 2
- Następny artykuł
- koniec






