W artykule przedstawiono projekt wstępnej stylizacji nadwozia pojazdu HEX-XT. Opisano różne etapy projektu, zaczynając od pierwszych szkiców koncepcyjnych, przez wstępny packaging i tworzenie modeli 3D, aż po wykonanie makiety pojazdu w podziałce 1:10. Makieta miała służyć do sprawdzenia proporcji nadwozia oraz stanowić uzupełnienie projektu stylizacji nadwozia.
Bartłomiej Błaszczak, Marian Ostrowski
Projekt HEX-XT ma na celu stworzenie pojazdu, który łączyłby cechy dwudrzwiowego samochodu sportowego oraz wyczynowego samochodu terenowego.
Po przygotowaniu pierwszej serii szkiców koncepcyjnych (Rys. 1), które uwzględniały wszystkie założenia projektowe, takie jak: nadwozie typu coupe, silnik umieszczony centralnie tuż za przednią osią, napęd na cztery koła oraz możliwie duże skoki zawieszenia, wybrano wersję do dalszego rozwoju.
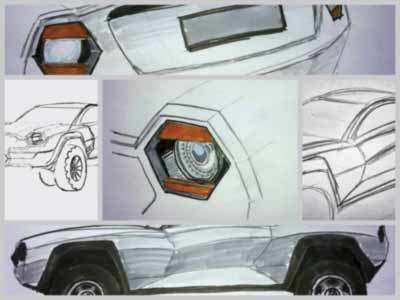
Rys. 1 Szkice koncepcyjne pojazdu HEX-XT
Przyjęto rozstaw osi, kół, a także wstępny packaging, uwzględniający najważniejsze podzespoły. Założenia zostały graficznie odwzorowane w programie SolidWorks i razem ze szkicami koncepcyjnymi były podstawą do stworzenia geometrii nadwozia w programie SolidThinking Evolve. Geometria nadwozia została zbudowana jako model powierzchniowy wykorzystujący między innymi krzywe NURBS (ang. Non-Uniform Rational B-Spline) (Rys. 2).
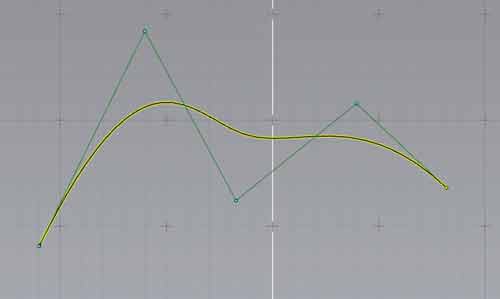
Rys. 2 Krzywa NURBS z widocznymi punktami kontrolnymi
Krzywe NURBS, czyli niejednorodne wymierne krzywe B-sklejane, składają się z fragmentów krzywych Beziera, których geneza sięga francuskiego przemysłu motoryzacyjnego lat 60-tych. Kształt tych krzywych w przestrzeni określa się za pomocą punktów kontrolnych, węzłów, wag punktów kontrolnych oraz stopnia wielomianów. Bazowe funkcje krzywych B-sklejanych zwykle oznacza się jako Ni,n, gdzie i odpowiada i-temu punktowi kontrolnemu, a n określa stopień funkcji.
Krzywą NURBS można opisać następującym równaniem: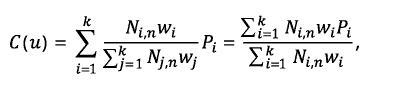
gdzie k to liczba punktów kontrolnych Pi, a wi to odpowiadające im wagi.
W przypadku, w którym wagi są równe jedności, mianownik również przyjmuje wartość jeden. W związku z tym sformułowanie można zapisać w formie: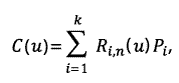
gdzie: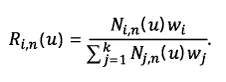
Funkcje Ri,n(u) nazywa się wymiernymi funkcjami bazowymi.
Powierzchnie NURBS powstają jako wynik mnożenia tensorowego dwóch krzywych NURBS, przez co mamy do czynienia z dwoma niezależnymi parametrami u i v. Powierzchnię NURBS można opisać następującą zależnością: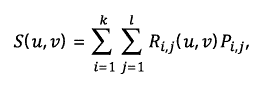
gdzie: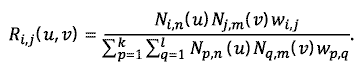
Funkcje Ri,j(u,v) podobnie jak dla krzywych nazywa się wymiernymi funkcjami bazowymi.
Właściwości krzywych i powierzchni NURBS powodują, iż świetnie nadają się do modelowania powierzchni o dużym stopniu złożoności. Ich plastyczna edycja pozwala na nadanie im pożądanego kształtu. W programie SolidThinking Evolve stworzono wstępną geometrię stylistyczną nadwozia, która została przedstawiona na rysunku 3.

Rys. 3 Wstępna geometria stylistyczna
Kolejnym krokiem było przygotowanie modelu nadwozia do wydruku 3D, przy wykorzystaniu technologii druku LPD. Zdecydowano się na wydruk modelu w podziałce 1:10 przy pomocy drukarki Zortrax M200 i materiału Z-Ultrat. Pole platformy wybranej drukarki to 200x200 mm, a maksymalna wysokość to 180 mm. W związku z tym, że wymiary modelu w podziałce 1:10 znaczenie przekraczają pole robocze drukarki, konieczny był podział modelu, na trzy części. Model uproszczono, usuwając detale których drukarka nie byłaby w stanie poprawnie wytworzyć. Następnie model powierzchniowy został doprowadzono do postaci bryłowej (Rys. 4).
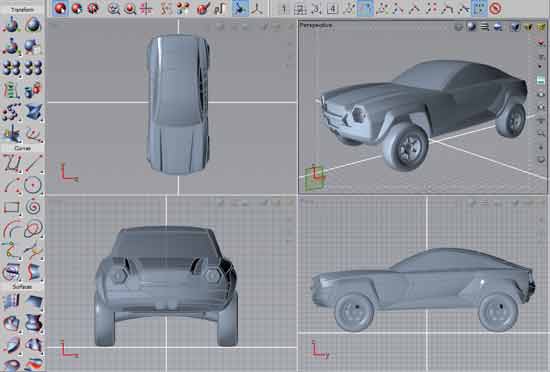
Rys. 4 Interfejs programu Evolve z widocznym, uproszczonym modelem bryłowym pojazdu HEX-XT
Ze względu na duże wymiary drukowanych elementów zdecydowano się na wydrążenie ich w taki sposób, aby zminimalizować objętość materiału. Do tego celu wykorzystano technikę CSG (ang. Constructive Solid Geometry). Jest to technika, w której definicja nowej bryły następuje poprzez wykonanie działania boolowskego na zbiorze brył składowych. Bryły te muszą się przenikać, aby wybrana operacja mogła zostać wykonana. Operacje boolowskie mogą polegać na sumie, różnicy lub części wspólnej brył. Przykłady tych operacji przedstawiono na rysunku 5.
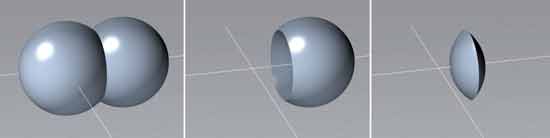
Rys. 5 Przykłady operacji boolowskich (suma, różnica oraz część wspólna)
Wydrążenie drukowanych elementów musiało zostać przeprowadzone w taki sposób, aby zminimalizować zużycie materiału podporowego. Pochylenie wewnętrznych ścianek, tak aby zbiegały się w jednym, najwyższym punkcie, pozwoliło na wydrukowanie zamkniętego elementu z minimalną ilością materiału podporowego.
- start
- Poprzedni artykuł
- 1
- 2
- Następny artykuł
- koniec






