Zjawisko fizyczne tarcia, powszechnie występujące w przyrodzie, ma duże znaczenie z punktu widzenia techniki. Towarzyszy przemieszczaniu się dwóch ciał względem siebie, powodując opory ruchu i wydzielanie ciepła, co negatywnie przekłada się na efektywność energetyczną w systemach mechanicznych. Oprócz strat energii potrzebnej na przezwyciężenie sił tarcia, stanowiących mniej więcej 30% światowego zużycia energii, tarcie odpowiada także za dodatkowe koszty związane ze zużyciem ciernym części maszyn i urządzeń, co przekłada się na konieczność naprawy lub wymiany komponentów, pochłaniającą około 5% PKB krajów rozwiniętych w skali roku. Nie ulega więc wątpliwości, że z opracowaniem doskonalszych sposobów na ograniczenie tarcia podczas działania maszyn i urządzeń wiązane są duże nadzieje. Jednym z obiecujących kierunków badań w naukach tribologicznych jest zjawisko nadsmarowności.
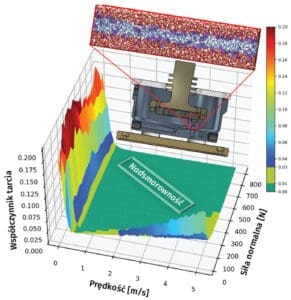
Nadsmarowność można zdefiniować jako stan, w którym tarcie pomiędzy elementami zanika lub jest pomijalnie niskie. Za umowną granicę nadsmarowności przyjmuje się współczynnik tarcia poniżej 0.01. Termin został po raz pierwszy zaproponowany przez japońskich badaczy Hirano i Shinjo w 1990 roku. W zależności od charakterystyki tribologicznej występuje:
- nadsmarowność sucha, inaczej strukturalna – na styku dwóch ciał stałych, między którymi zachodzi tarcie suche;
- nadsmarowność płynna – w obecności środka smarującego na styku dwóch ciał stałych, przekształcającego suche tarcie zewnętrzne ciał stałych w wewnętrzne tarcie cieczy;
- nadsmarowność mieszana – w warunkach tarcia granicznego lub elastohydrodynamicznego, również w obecności w środku smarnym nanostrukturalnych napełniaczy, pozwalających na zwiększenie przenoszonych obciążeń.
Zasadniczo w mechanice przyjmuje się, że współczynnik tarcia zmniejsza się wraz z redukcją chropowatości powierzchni. Jednak punktem wyjścia dla badań nad nadsmarownością suchą było powiązanie tarcia z oddziaływaniami na poziomie atomowym, a więc w ramach struktury krystalicznej.
cały artykuł jest dostępny w wydaniu 3/4 (210/211) marzec/kwiecień 2025